FROM PLATO TO NEWTON
[The following also serves as an introduction to the Background section of the separate Webpage: 'The Problems Addressed by Einstein...' (where it occurs as an Appendix) or it may be consulted as here - as a separate Webpage of its own.]
In the summer of 1684, Isaac Newton, then Professor of Mathematics at Cambridge, was visited by the future Astronomer Royal, Edmund Halley, to discuss current ideas on 'celestial mechanics'. Some 70 years earlier, Johannes Kepler in Germany had carefully analysed the mass of observations then recently made by the Dane Tycho Brahe on the movements of the planets and found them to have slightly elliptical orbits around the Sun, and not the circular ones previously assumed. The consistency of his findings led him to generalise three empirical 'laws' on this subject, although he was the first to admit he had no theoretical explanation to account for these findings - which overturned long-accepted views by Aristotle and Ptolemy. Some powerful celestial 'force' seemed to be responsible for such orbits but in the early 17th century, no one had a very clear conception of its nature or source. The underlying physical principles at work were largely unknown.
By the 1680s, however, it was being suggested by various contemporary thinkers that this previously unrealised motion of the planets might be due in part to a major force emanating from the Sun - one which appeared to weaken rapidly as the distance from the Sun to any planet increased. But no one had been able to affirm this idea with a rational explanation. Thus, during his visit, Halley asked Newton what he thought about the problem and was surprised to hear Newton say he had already sorted it out, having accounted precisely for Kepler's findings in terms of just such a force, centred on the Sun, which did indeed diminish rapidly with distance. He had given similar thought to the mutual forces that appeared to attract the Earth and Moon to each other (or at least kept the latter in its orbit). He claimed he had mislaid the crucial proof, but told Halley he could work it out again and send it to him. He may have wanted to clarify some aspects.
A few months later, true to his word, Newton sent Halley a short treatise in which he showed that the Sun's suspected force would largely account not only for Kepler's elliptical orbits but for his other empirical laws of planetary motion as well. Halley soon realised that this was a key to understanding the workings of the universe as it was then known. He urged Newton to publish at once but Newton felt it needed further development and so worked on certain implications over the next 3 years. In 1687, at Halley's expense, Newton's masterpiece - 'Philosophie Naturalis Principia Mathematica' - was finally published - the work on which modern physical science was to be based for over two hundred and fifty years. Einstein was later to say that Newton's Principia was "perhaps the greatest intellectual stride it has been granted to any man to make". It put into a unified, coherent form many disparate facts and principles that had accumulated from earlier times, but never truly understood. [One wonders if Halley appreciated that the 'workings of the Universe' implicit in Newton's explanations of Kepler's findings would in fact prove as comprehensive in application as it did? It would certainly generalise to much more than 'celestial mechanics' alone.]
Newton said that if he saw further than most, it was because he was able to stand upon the shoulders of giants who went before him. The first of these was Copernicus whose ideas replaced those which had been accepted for over a thousand years - since the time of three earlier giants of ancient Greece. There follows a brief resume of the contributions of these several great thinkers on these fundamental questions.
1. Plato
The early Greek philosophers had views on most things and certainly a giant amongst these was Plato. In the 4th century B.C., he devised a scheme of physical reality in which the world was at the centre of a series of perfect circular spheres in which all heavenly bodies moved in circular orbits. This was an idealised world view based on the most perfect of forms - the circle and the sphere. It relied upon observation and conjecture - as does all science. It was a necessary beginning. And because Plato was so respected, this view held sway for many centuries. However, no basis was proffered for any forces that might underlie or account for such movement.
2. Aristotle
Aristotle developed Plato's scheme further - conceiving the universe as consisting of four basic elements or 'essences'; the earth at the centre, surrounded by water, then air and finally fire in ascending spheres. Natural motion occurred, he claimed, when these elements 'tended to find their natural place' in this arrangement. Thus earth, rock, minerals, etc sank (fell) through air or water while bubbles of air or other gases rose up through it and smoke and fire, in turn, rose through the air. All other motions were seen as violating these natural movements (with an implication of gravity) and occurred when some immediate, proximate cause impressed itself upon any object, as when a horse pulled a cart. Beyond these four elemental spheres were the celestial ones composed of a fifth or 'quint-essence' in which the heavenly bodies revolved around the world at constant speed in perfect circles. Thus, these early attempts to understand the nature of the universe, of its 'workings', focused essentially upon 'movement'. This is of course as should be expected; without movement, nothing happens and there would be nothing to enquire into or explain. But what causes such movement and what laws control it? This was the beginnings of 'classical mechanics' - the fundamental core of that most basic of sciences - physics.
Aristotle's conception was upset somewhat by the fact that careful observation showed that the planets didn't quite follow perfect circles but because Plato's view was still accepted, their orbits were said to be centred within yet other truly circular paths which seemed to correct for this anomaly.
3. Ptolemy (c100-170)
The Platonic-Aristotlean system of astronomy, with its corrective circles within circles (today called a 'Fourier series'), was further refined and codified by Ptolemy of Alexandria in the 2nd century A.D. in his classic book - the Almagest. This remained the accepted textbook of astronomy for fourteen hundred years - that is, until the time of Copernicus. With it, continued also the unquestioned acceptance that the basic motion here on Earth - falling - was due simply to things tending to find their natural place - towards the earthly centre of the universe. This geo-centric view of astronomy and mechanics accorded well with the teachings of the Christian church, centred in Rome, which had become the accepted authority in all such matters throughout Europe. God had somehow favoured the Earth as a true centre of all things. [Thanks to various Arabic scholars, much of the science of the ancient Greek and Eastern world was preserved and translated around 1000 AD at the library in Cordoba in Moorish Spain. Much of this, otherwise lost during the 'dark ages', was thus available for later thinkers in Europe.]
4. Copernicus (1472-1543)
The need for the awkward system of corrective circles could however be largely removed, said Copernicus, a brilliant Polish priest, if one placed the Sun as a fixed reference 'point' at the centre of the universe - rather than the Earth, or the so-called 'fixed stars' - thus relegating the Earth to being 'just another (moving) planet'. He maintained publicly that this adjustment was merely for mathematical convenience when working out positions and orbits of the planets (of concern to agriculture and navigation) - still of the ideal circular form - but this appears to have been a cover for his true convictions. Fearing the church might not accept his new conception of astronomy in which the Earth lost its primacy (written in 1530), Copernicus delayed publication of his famous book 'De Revolutionibus Orbium Coelestium' - until shortly before his death in 1543. It would eventually overturn our long held convictions about our assumed primacy in the universe as promulgated especially by the church.
5. Tycho Brahe (1546-1601)
Twenty years after Copernicus died, during which time little attention was paid to his revolutionary ideas or his book, young Tycho Brahe, a Danish nobleman with time to spare, became interested in observing events in the heavens - including solar eclipses and the conjunction of planets. He noticed that most tables concerned with these events were quite inaccurate, including even those of Copernicus. He continued to observe carefully and soon discovered a new star - something not expected in terms of the ancient schemes of Aristotle and Ptolemy. He was then given Royal support - first by his own King and later by Rudolph, the Holy Roman Emperor in Prague. His readings of Copernicus did persuade him that some revision of Ptolemy might well be required and so devised a new cosmology which, in contrast to Copernicus, returned the Earth to the centre. He conceded that the planets did revolve around the Sun, as Copernicus maintained, but that the Sun, with these revolving planets, then revolved 'en mass' around the Earth. It was a compromise between the cosmologies of Ptolemy and Copernicus. He made, without the aid of telescopes, hundreds of vital observations in an attempt to justify this new conception but did not possess the mathematical skill to analyse properly all his data. In all Europe, there was probably only one person with this ability:
6. Johannes Kepler (1571-1630)
Kepler was from a poor German family but displayed exceptional intelligence and won a scholarship to Tubingen university where he learned of Copernicus's alternative world view. He was convinced of its essential validity and by 1595 devised a model of the planetary orbits which best fitted most known facts about them. He noted certain regularities in the ratios of the diameters of different orbits, involving considerable calculation, and published his views in a book 'Mysterium Cosmographicum'. This was brought to the attention of Tycho Brahe who realised that Kepler had the mathematical skills to more thoroughly analyse his own data. He asked him to join him at Prague, which he did - in 1600. Kepler began organising Brahe's extensive data but was not quite persuaded that it supported the latter's conception of the universe. Brahe was soon to die - in 1601; Kepler remained in Prague as the new Imperial Mathematician for Emperor Rudolph and began re-analysing Brahe's data - but more in terms of his own Copernican model. Over the next 25 years, he worked out his three empirical laws of planetary motion which proved reliable and consistent. Usefully, the telescope was invented during this time.
But early in this period, Kepler found great difficulty in fitting the path of Mars into its expected circular orbit. Prior to Brahe, the uncertainty in the measurements of planetary observations was of the order of 10 minutes of arc. Within this degree of error, Kepler found he could calculate the path of Mars as a circular orbit, even after adjusting for the fact that Brahe's data had now, in Kepler's new scheme, to take account of its measurement from a planet (Earth) that was itself in orbit. But now, with Brahe's more accurate observations, this degree of error was no longer tolerable and no amount of Kelpler's prodigious calculations could fit Mars into the exact circular orbit that he (following Copernicus) believed it had. He did find, however, that he could describe the path of the Earth itself as a virtual circle, if he placed the Sun slightly off the centre point of such an orbit. He tried to make a similar adjustment for Mars, but it's orbit would still not be persuaded into such a circle or even near circle.
At this point, Kepler apparently recalled the views of the ancient Greeks that the Earth, unlike the distant, 'true' planets, was not in their state of untrammelled perfection - since it supported organic life and showed change and decay over time. But if he was right and it too was truly 'just' a planet, maybe all of them displayed imperfections such that none of them need be constrained into the idealised Platonic or even Copernican circles after all. He then shifted the position of the Sun in relation to the orbit of Mars even further from the idealised centre - calling this new position its 'focus' (from the Greek for 'a place of fire') - and quickly concluded that the correct orbits for all planets weren't in fact circles after all - but ellipses. He published his new findings in 'Astronomia Nova' in 1609, when he showed that the orbits of all the planets, including the Earth, were indeed ellipses, with the Sun in each case occupying the position of an off-centre focal point. This assertion, based on detailed empirical analysis, became known as Kepler's first law of planetary motion - or the law of ellipses. His observations and calculations also discovered another consistency in the nature of the cosmos - namely that when the planet is further from the Sun in its elliptical orbit it moves more slowly than when it is nearer that focal point. And while it moves at this slower speed at its more distant path, it covers (sweeps across) a greater area between itself and the Sun, and conversely so when nearer the Sun. If the time for such coverage of these areas of arc is made equal, the areas covered would thus also be equal, despite the different speeds of the planet in these different parts of its orbit. This became known as his second law. Finally, ten years later, he expounded a third law - in his book 'Harmonices Mundi'. In this, he considered not planets generally but compared the size of particular individual orbits. He discovered that the greater the orbit, the slower a given planet travelled and that its speed was proportional to that orbit - specifically to a particular measure of the orbit (comparable to its radius) - raised to the power of 3/2. [This can also be expressed in other ways.]
Kepler summed up his own findings, and Brahe's meticulous observations, in a book of tables entitled the 'Rudolphine Tables' in 1627. This provided the scientific world with the first really accurate basis of astronomy and navigation and, significantly, an inspiration to later thinkers, especially Newton. Kepler realised that he could not account for his empirical findings on planetary orbits by any known general principles and that further work was required. He did suggest that some 'influence' emanating from the Sun may somehow be involved but did not attempt any quantitative analysis of this idea - to which Newton would one day apply himself. But first, there was a contemporary of Kepler whose contributions were to be just as vital; another shoulder-possessing 'giant':
7. Galileo Galilei (1564-1642)
Another early advocate of Copernicus was Galileo who, like Kepler, was of a mathematical bent and earned his early living by lecturing in this subject - at Pisa University. He became well known after his early discoveries in the sphere of 'forces' - in his laws of 'fall' and of 'pendular motion'. He believed in the essential validity of Copernicus (as did Kepler) but kept his views to himself, or expressed them ambiguously for fear of persecution by the church. Kepler sent him a copy of his book 'Mysterium Cosmographicum' in 1597 and in his thank you note, Galileo said he was pleased to find a friend in science who was also 'a friend of Truth' - apparently a disguised reference to Copernicus - if not to an objective approach to science By the early 1600s, the church had put Copernicus's book on its banned list, claiming its main thesis to be erroneous. And common sense seemed to support the church; Copernicus said the Earth spun on its axis - once every 24 hours - so that it was the Earth that moved (from west to east) and not the Sun - in the opposite direction, as it clearly appeared to do. Moreover, he said that the Earth also revolved, like the other planets, around the Sun - thus providing it with yet more alleged movement - of which again no one on the Earth was in the slightest aware. And, in any case, surely God put the earth at the centre of things.
If Copernicus was right, therefore, how could this be shown? This was the challenge Galileo was faced with. He had somehow to overcome a very compelling reality: If the earth really moved as Copernicus said, its speed could be easily calculated - to be some thousands of miles per hour (ie in relation to the Sun). Not only was no one aware of such alleged motion, but it should be testable by dropping some object from a high tower - such as the famous one at Pisa - and observing whether, as it fell under the influence of gravity (then still just a name given to Aristotle's natural motion where objects tend to 'find there own place'), the Earth with the tower attached to it, moved at speed its predicted distance for that period so that instead of the object landing near the foot of the tower, it should land some miles behind the 'new' position of the Earth and Tower. Of course, it didn't behave that way, but landed at the foot of the tower. Why was this? The church said it was because the Earth did not in fact move as the object fell - but was the solid, stationary centre of the universe around which everything else moved and on which things naturally fell towards its centre. How to disprove this? (And show that the object was already moving horizontally - with the earth - before it was released.)
Galileo decided the best thing he could do was to learn much more about falling objects generally - by measuring the details of such actions more precisely than anyone had previously thought necessary - as objects allegedly found their 'natural place'. By this means, he discovered that objects fell at the same accelerating speed whatever their size or weight - when one accounted for the effects of air pressure. The distance travelled increased per unit time as the square of the time and did so uniformly. This was his 'law of falling bodies' and resulted from one of mankind's first planned experiments as a way of gaining knowledge. [There was however an important early Arabic experimenter at Alexandria. I believe - ca 1000 AD.] Because bodies fell vertically so quickly and timing methods were then quite inaccurate, Galileo made use of a range of very smooth inclined planes down which polished metal balls were rolled. The times taken for their descent was thereby sufficiently slowed to allow accurate 'falling' measurements. He found that such balls would, after rolling down such a plane and displaying the acceleration that he discovered, then roll up another slope, with which it was in direct continuity, until it reached the same height as that at which it started. If the slope of the rising plane was gradually reduced, the balls kept rolling longer until eventually achieving their original height, even if this was very gradually over quite a distance.
One of the most fundamental and profound laws of nature was then discovered by Galileo. For he reasoned that after a ball had been given its initial impetus by rolling down such a sloping plane (through the energy available from the force of gravity), if the continuing tracks on which it was rolling did not then begin to slope upwards, even gradually, but remained absolutely level, the ball would (if friction and air pressure are ignored) roll on, and at a constant speed, forever! This was at variance with the ideas of Aristotle who felt that except for objects seeking out their natural place (as falling down), any such horizontal motion was only possible where there was an immediate (proximate) and oft-repeated force applied; otherwise it would stop. But it appeared that the initial force applied to a movable object remained with it (as a transfer of energy) permanently - unless opposed by an equal and opposite force. This finding or conclusion by Galileo was eventually to be formalised by Newton as his first law of motion - the law of inertia: 'Any object either remains at rest or continues in a state of constant motion (ie forever) - unless acted upon by some other force'. A force is thus that which opposes inertia and 'changes motion' - ie causes 'acceleration' or 'deceleration'. Much of physics follows from this basic law.
Amazingly, this fundamental principle, arrived at by Galileo through his methodical probing of such a basic phenomenon as falling objects, provided the clue to resolving both of the problems he started with - that is, why no one senses any movement of the earth despite its claimed speed of both rotation and revolution, and why a tower and the earth to which it is attached doesn't move several miles away from an object dropped from it while in free fall, before reaching that (fast-moving) ground. For the earth and everything attached to it, including not only the tower but the object itself (about to be dropped), are already all moving together - under the influence of their shared inertia due to whatever prior force initiated same. And after the object is dropped, this impetus, by the law of inertia, continues to act upon it also - throughout its period of falling - such that it remains next to the tower as both the object and the tower continue to sail horizontally through space together (despite being unjoined) each with their respective, pre-existing inertias. While the additional force of gravity admittedly does now act also - to pull the object to the ground - it does so quite independently, pulling it vertically down parallel to the (comparably-moving) tower without interfering with the on-going horizontal movement of the object as it, and the tower, continue to move in that shared plane in unison - ie with the Earth. Similarly, all sentient beings on earth, born as we are into our already fast-moving world, continue moving with it with no sense of varying acceleration or deceleration - under the influence of an unperceived inertia - quite unaware of our immense on-going speed of revolution (relative to the Sun) nor our rotation (relative to our own axis).
Galileo's two laws thus provided an exact explanation of what occurs when, for example, a cannon ball is fired. Once given its initial impetus by the exploding gunpowder, it should (if one ignores air pressure and friction) continue horizontally at a constant speed (law of inertia) - after its initial acceleration - for as long as it remains air borne; that is, until the law of fall (due to gravity) - acting as it does in the vertical plane - brings it to earth. He showed that the trajectory of such a projectile, long known to be of a curved nature, was in fact a compound of these two forces - in the form of a parabola (again ignoring air pressure). He seemed to sense that this form, like the ellipse noted by Kepler, being two of the four classical 'conic sections', could hold some fundamental significance in unravelling the secrets of nature. Galileo wrote up these thoughts in his book called 'Two New Sciences' in 1638. This was very prescient; Newton was to open up the power of science by applying exactly these two principles of Galileo - one of those indeed on whose high and broad shoulders he in particular was later to see further and more clearly than anyone of his day (or many a day).
8. Rene Descartes (1596-1650)
One more crucial advance was needed however before Newton could formulate his masterly synthesis. Galileo was not quite ready to abandon the almost unconcious influence of Plato; when he conceived his law of (horizontal) inertia, it was within the constraints of a global environment. An object would continue indefinitely in a given direction parallel to the earth's surface - ie globally and thus becomes not motion 'in a (truly) straight line' but in effect 'circular motion'. In France, Rene Descartes appreciated that the effect of inertia should be in a truly straight line only. It was in this form that Newton was able to formalise this principle as part of his famous set of laws of physics in 1687. Descartes, like Brahe, also attempted to re-cast the Copernican world view into something more acceptable to the Catholic church but it proved to be unsustainable in logic. The discoveries of Copernicus, Brahe, Kepler and Galileo were thus to be combined finally by Newton, but Descartes did put into place that important late piece of the puzzle - the necessary true straightness of inertia. [But in relation to what?]
Isaac Newton (1643-1727)
Much of Newton's work was done during the 1660s and '70s - both in Cambridge and at his home estate in Lincolnshire during several 'plague years' - when the curriculum in such a conservative institution was still dominated by Aristotle's conceptions of the nature of the universe. The work and writings of the five giants described above were not shared and disseminated with anything like the manner of science today or even during the coming 18th century. Such works, usually written in Latin (via those Cordoban translations?), had to be sought out and analysed within prevailing conceptions and limitations. We view all these matters from hindsight - having taken 'on-board' conclusions that in those days were often suspect hypotheses, with many gaps and uncertainties. By about 1685 or so, Newton was, with the help of Galileo's findings, ready to challenge and replace the Aristotlian world view with his own elegant solution to the unrealised potentialities provided by such forerunners. This came about when he sought to answer the question: Is there a set of general rules or principles of nature, concerning an interaction of forces, bodies and movement, which will adequately explain or account for Kepler's empirical observations of the motion of planets? And if so, will they not account equally for all other activity (motion) within the universe, both microscopic and macroscopic, including Galileo's laws of Fall and of the Pendulum? How to account for a parabolic trajectory of a canon ball as influenced by two forces acting at right angles and an elliptical trajectory of a planet - acting under unknown forces? Newton would apply a more precise quantitative analysis to Galileo's partly qualitative findings, based on a few simple motions, and then generalise his conclusions to all motion. This quantitative analysis took him many years of concentrated mental manipulations - the work of a true genius of immense mental powers and determination.
Newton was able eventually to reduce the ideas and empirical findings of the previous century, coupled with new postulates of his own, into a set of just three rules or laws by which such questions could be answered. The first concerned inertia: 'Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it'. The second law describes what happens if such a force does so act: 'The change in motion (thus arising) is proportional to the motive force impressed and is made in the direction of the straight line in which that force is impressed'. By 'change in motion', Newton apparently implied a change in the 'amount of motion' rather than just its change in direction, since this latter aspect is addressed separately in the second part of this law.
The prior motion of a body - before a new force acts upon it - is, in terms of the 'amount' of such motion, a function of its then speed (or 'velocity' if its direction is specified) and the amount (mass) of that body moving with that speed. Where this amount of a body's previous, on-going 'motion' is altered by a newly acting force, the change (say an increase) of that amount of motion is in this sense proportional to the (increased) magnitude of the new force so acting. This 'change in (amount of) motion' would today be referred to as an increase in 'momentum'. Implicit in Newton's second law is the very fundamental definition of that most mysterious of phenomena - 'force' - which is today measured in terms of 'mass x acceleration', where acceleration implies an on-going change (increase) in the velocity of a body - ie an increase in amount of motion or momentum. We still do not know what 'force' is; we only know what it does and thus can only define it in those terms; it is that 'influence' which does this: it causes a mass to accelerate or decelerate - ie to change its velocity - including, possibly, its direction. Certain changes of speed and direction (in the form of say an ellipse or a parabola) may arise through the joint application of two or more such influencing forces.
Newton's third law states: 'For every action there is always an equal reaction; or the mutual actions of two bodies upon each other are always equal, and are directed to contrary parts'. By 'actions' and 'reactions', Newton seems to signify the effects of the forces implied in 'bodies in motion'. This law too has its important implications. In particular, it recognises that all bodies and more obviously very large bodies such as planets in motion possess inherent sub-forces within and between themselves which conveniently cancel out such that each can be treated as though their masses were concentrated at a point at their respective centres. [This law needs further analysis on my part; it seems to have been formulated and its fundamental reality accepted in order that anomalies arising otherwise could be eliminated. The first two laws seem relatively self-evident in terms of their prior evolution but this third one is less obvious to me. How did he arrive at it? One will just accept it for now.]
These three laws are thus concerned with 'forces acting upon bodies' - and their resultant 'movements' - ie with the 'dynamics' or 'mechanics' of nature - and as such replaced the ideas of Aristotle on 'natural' and 'unnatural' motions in this fundamental sphere of science and nature. He complemented these three laws by specifying one major force - that acting between all bodies: the force of gravity - with its virtually immovable centre concentrated (in theory) at the centre of the Sun (although all bodies 'engender' gravity). He would use the second and third laws of Kepler to deduce two important properties of this fundamental force and then, in what must comprise the most profound and important of all his discoveries, Newton established the validity of his three laws and his conception of the force of gravity centred in particular on the Sun by showing that together they (and seemingly they alone) could precisely account for Kepler's empirically established first law - describing the elliptical orbits of the planets around the Sun - that empirical reality of nature that required explanation in terms of some more general principles of the universe of nature.
Newton didn't just 'think up' his 3 laws in isolation, therefore, and then recall that, conveniently, someone had already observed an aspect of nature on which such 'theoretical' general laws could be properly tested and hopefully verified. Rather, he was only able to postulate and/or deduce his laws in the first place on the basis of an intimate analysis of Kepler's prior empirical findings. In this sense, he didn't prove the validity of such elliptical orbits; their validity was already established empirically. But he was able to show that Kepler's first law was really a consequence of the latter's second and third laws since it was they on which the implication of gravity as a Sun-determined force was based and which would eventually be shown to account for the elliptical orbits. Only the general concept of Gravity and properties deduced for it, can do this. It is thereby accepted as a fundamental reality or principle of nature. It alone works - in accounting for known empirical data. [Much later, Einstein, in turn, would provide an even more general/fundamental way of accounting for gravity.]
As each of Newton's predecessors chipped away at the former Aristotlean world view, there was still left a buzzing confusion - without the remotest hint of how it might be replaced. Descartes tried but failed. Finally Newton worked it out and gave it a coherent, valid form; that 'greatest intellectual stride' referred to by Einstein. And the proof that he was right occurred when he was able to show that his carefully formulated general laws of nature, and only these (with gravity), would account exactly for Kepler's empirical law of planetary ellipses - which described how nature actually behaved. Their validity was thereby fully supported. Other fundamental trajectories - such as those of the parabola and hyperbola - could be accounted for in similar terms.
Newton's Famous Proof.
Newton demonstrated (ie accounted for) Kepler's ellipses by a geometrical proof which relied upon the dynamic features of his new laws and ideas on gravity as expressed in the Principia. In so doing, he utilised certain accepted and proven geometrical principles pertaining to conic sections much understood by himself and his 17th century colleagues. These are rather obscure today and thus, in a demonstration to a class of Physics undergraduates at the University of California in 1964, the famous American Nobel prize winner Richard Feynman reproduced Newton's 'proof' in which these more obscure aspects were replaced with a more contemporary geometric reasoning. This lecture was subsequently 'lost' for many years but was eventually re-discovered and, in 1996, published in a book entitled 'Feynman's Lost Lecture' - by David & Judith Goodstein, fellow physicists. Most of this present account comes from this excellent little book as does the following resume of the famous proof ; it combines elements from both the Goodsteins' own re-drafting of Feynman's lecture (as he apparently tended when talking to rush the explanation of some of his reasoning) and from Feynman's lecture itself. Most of it is quite simple and straightforward but the latter portion, based on Feynman's alternative reasoning, is more complicated and lengthy (and may be condensed here). He described it himself as 'elementary' in the sense that its logic was introduced (to the student) within its own development.
Feynman (and the Goodsteins) begin by pointing out that before proceeding to establish/demonstrate that a particular interaction of moving bodies and forces, as those asserted in Newton's laws, should result in (ie account for) a certain form of planetary motion - namely an elliptical orbit - it is necessary first to agree on just what an ellipse is; what its geometric properties are. If, then, the demonstration succeeds in establishing that the application of those laws results in the relevant bodies (planets) following paths of this agreed and understood form (as established by Kepler), the correctness or validity of those laws can be accepted with confidence. However, as one can not apply them to the actual planets, this must be done by means of geometrical proofs based on two-dimensional drawings and associated reasoning which rely on meeting such criteria concerning these accepted properties of ellipses.
Kepler certainly knew what an ellipse was, just as he knew what circles, parabolas and other sections taken across a cone were. These were much in vogue in his day. Feynman points out that there are several ways to create an ellipse and demonstrates three of these as a means of exemplifying the essential properties of an ellipse, properties which in effect define it - which is his first objective. The first and traditional way is by drawing an ellipse on paper using a pencil, string and two tacks. Before doing this here, it might be useful to first describe how to draw a circle by similar means. Using a loop of string with a pencil pulling the loop taut at one end and the other looped around a tack placed in the middle of a piece of stiff paper, a circle can be drawn with a radius equal to the length of the doubled string (or diameter equal to the full length of the loop) - say about 6 inches. As the pencil draws the line - eg in an anti-clockwise direction - at the top of its curve the line is, momentarily, moving from right to left. The force impelling it in that direction, at that moment, is the drawer's hand and associated musculature. That it doesn't continue to move in a straight line further and further to the left is due to another force acting equally continuously on it. This is the taut string constantly held at the centre of the developing circle by the tack. In a sense, this force is directed via the string back to that centre point, or at least it's in a certain balance with the muscular force. The combination of these two sets of forces acting on the pencil results in the drawn circle. Planetary bodies in nature could be seen as moving in a circular or near circular path due to the influence of two similarly directed forces.
If now we push in a second tack a little to the right of the first one (say half an inch), cut the string and tie one end to the original tack and the other to the new tack such that the total length of the string is the same as before and re-draw the 'circle', it will be seen that at the top of the curve, and at the bottom, the path of the curve is virtually identical to the first one drawn, being possibly very slightly inside the original lines at these points. But at the leftmost and rightmost points, the lines will be more clearly outside the original path. This is because the length of the doubled string going from the first tack to the rightmost point on the original circle and back to the second tack (to the right of the first and thus closer to the circle) is now longer than required (to copy the first circle exactly) and when the pencil pulls it out to its full taut length, it is half that extra half an inch longer - on each (right and left) extreme point and proportionately less as the line re-joins the top and bottom parts of this now not quite circular 'orbit'. This new shape is an ellipse. True, it is one that appears to be almost a circle but this is because its two 'focal points' have been chosen to be fairly close together. In fact, if they were to coincide exactly, the resultant 'ellipse' would be a true circle which, by this definition, would be but a special case of an ellipse - one in which the two foci exactly coincide.
If a cone is cut across parallel with its base, the resulting cross section would be a circle. If that cut were made at a slight angle to the base, the result would be an ellipse and no doubt there is some mathematical relationship between the distance chosen between the two tacks in the drawn example and the degree of slope of the sectioned cone for a given ellipse. [By some alchemy which this writer does not yet understand, there is a mysterious correspondence between the static geometric forms obtained when a particular shape in nature - a cone - is sectioned, ie a circle, an ellipse, a parabola and a hyperbola (from a 'double cone'), and these same forms when they arise as orbital paths by the interaction of certain forces (often two in number) with some body/object/particle moving in nature. There must be some correspondence between the dimensions or shapes of a cone and the angles at which forces act. This aspect is touched on further at the end of the proof.]
When the two lengths of string join the two, separated tack points, each can be viewed as providing the same kind of pulling force on the pencil back towards their respective 'centres' (focal points) as the doubled string did back to the single centre in the earlier example. That is, they constrain the path of the pencil in such a way that it describes a form known as an ellipse. The farther apart the two tacks, the more elongated the ellipse. Ellipses can thus be of many different shapes but with a basic, symmetric form dictated by the two-focal-point characteristic described. That is the fundamental characteristic of their nature and production.
Feynman then defines an ellipse secondly in a more abstract geometric way as the set of all points that can exist at points P which occur at the junction of two lines which originate at these two separated focal points such that their total, combined length remains a constant at all possible orientations of such lines when meeting at those points. A third and apparently equivalent definition is that light emanating from either of these focal points and directed to any one of such points P as together comprise the ellipse will be reflected back precisely to the other focal point - ie at the same angle. This implies that at every such point a mirror-like tangent can be assumed which allows just such a reflection. Feynman provides a proof of this equivalence which we may accept here without elaboration.
An additional, fourth property of the ellipse is then described which Feynman says is important in the proof and which he will need to use later in his demonstration. It is necessary because of the difficulty he had in following Newton's use of certain aspects of the conic sections referred to earlier. In place of this, he has devised an equivalent proof which relies upon this additional property of an ellipse - one which follows from the ellipse's foregoing property of tangential reflection of light. For this purpose, an ellipse is defined as the shape that results when a specified point on a series of tangents to a curve are joined - where such tangents arise as perpendicular lines crossing a line running between a point on an enveloping circle and a focal point within that circle, the centre of which serves as a second focal point. A line drawn from either focal point to such tangents if reflected at the same angle will meet the other focal point (as in the 3rd property described above). Feynman would later show that such an outer circle can be so constructed to represent a continuity of planetary velocity changes which, in terms of Newton's laws and gravity, can only have arisen from a planetary orbit which proves to be an ellipse according to the above definition or property. That is, if the changing speed of a planet as it traverses an elliptical path is represented geometrically it 'adjusts' the elliptical shape into that of a circle. The variation in its speed must reflect (correlate with) the distance between the two focal points of the ellipse.
Proving Kepler's Laws.
The foregoing provides us with sufficient definition and description of the ellipse and its properties to constitute the objective to be realised when one applies Newton's laws of dynamics to (geometric representations of) planets orbiting the Sun in ways described by Kepler. One may draw a circle or ellipse as static geometric forms whose relationships can be analysed logically but ultimately these must represent the paths of orbiting planets actually moving in three dimensional space under the influence of known astronomical forces.
Feynman begins, as did Copernicus, Galileo, Kepler and Newton, by accepting that planets, including the Earth, are indeed moving (in particular around the Sun) and that part at least of that movement can be accounted for by Newton's 1st law - concerning inertia. If planets, given some initial impetus, were influenced by no other forces, they should, according to the law of inertia, continue such movement in a straight rather than curved orbital line and continue so indefinitely. To be moving at all, as all planets certainly appear to be doing, implies that there must have been some initial force or impetus acting on them in the past, even briefly. For such motion to continue, however, no subsequent on-going or intermittent forces are needed; inertia itself (as a transfer and continuation of the initial impetus) is sufficient to maintain indefinitely their obvious movements across the sky - at least in that theoretical straight line - unless and until subjected to any additional force(s).
If the law of inertia provides a rationale for the continued movement per se of planets and specifically for that (masked) straight part of their motion, what can account for any other part - which results in the curved paths actually observed? Newton reasoned that whether its actual motion was circular or elliptical, the tendency for a planet to continue moving otherwise - in a straight line - would be appropriately offset from same and 'forced' into one or other curved path or orbit, if they were under the additional influence of a force pulling them directly towards the centre of its orbit (typically the Sun) - just as the taut string does in the drawing. One of Newton's crucial conclusions based upon the works of Kepler and Galileo was that the strength of such a force, directed towards the Sun, diminishes rapidly across space. However, this conclusion by Newton was apparently not vital for the initial part of his proof, which actually dealt with Kepler's second and third laws, although would become relevant and necessary in respect of the crucial proof of the first law - concerning the elliptical form of such orbits (discussed later). For now, all that was required was that there was a force - of whatever strength or variability - that was directed towards the Sun and which could account for a non-straight (ie curved) orbit. To account for Kepler's 2nd law, Newton reasoned that his own first two laws would provide an adequate explanation, if he also posited the existence of such a force, simply with the direction of action required, regardless of any changing strength over distance it may or may not be shown later to have.
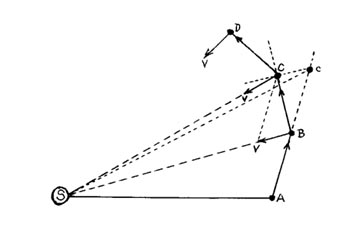
Feynman follows Newton exactly in the first part of this geometric demonstration (proof). He depicts a planet travelling anti-clockwise around the Sun beginning at an arbitrary point A some distance to the right of the Sun (or rather its geometric representation). He argues that with no other force acting upon it except its own inertia, it would indeed continue along a straight line from this point A, a line that would be the tangent at that point if it were a circular or near circular path were some other force applying to account for such. After a given time, the planet would then be at a new position B and after another, equal period of time, with only inertia acting on it, it would arrive at a third position 'c', where the line A through B to 'c' would be a continuation of the straight line A-B. ie:

However, the actual trajectory of the planet is the outcome, says Newton, of a competition between the two forces acting upon it - its inertia and the pull of the Sun's gravity. Hence, as it attempts to travel from A through B towards 'c', due to its inertia, it is also being acted on continuously by the Sun's gravity, throughout that time. If the effect of the latter force is however only shown at the end of each period (ie the period depicted by A-B in the first instance), as though its action was 'saved up' ready to affect the trajectory over its subsequent interval (rather than as it actual does smoothly throughout), then the true position of the planet after the interval B-'c' must take account also of this added, on-going component of its motion, a component directed back towards the Sun. This part of the force is depicted by the line B-V. The effect of the combined action of inertia acting over the component B-c and the Sun's force in the direction B-V is compounded into a parallelogram B-c-C-V - with its diagonal B-C representing the resultant 'actual' path of the planet. [This is the first corollary to Newton's laws.] The correction in the 'inertia only' path is thus the distance c-C - which equals that of B-V to which it is parallel. Note that being parallel, its extension centrally would not meet the focal point at the Sun's centre, as that of B-V would, as it occurs further along the orbit.
This same analysis can be made for all subsequent equal intervals of time such that the path of the planet assumes that of a polygon A-B-C-D-E etc. Each time interval (A-B, B-C, C-D, etc) is the same although the distance covered in these may well differ (where the speed varies). While the position of the planet on any drawn orbit represents its position in space, the orbit can be divided up in terms of distance, time or velocity changes. If it's in terms of any one of these, the others would have to be imagined. In any case, if the equal time intervals are made increasingly shorter then, in the limit, the polygon becomes a circle (or possibly an ellipse; see later) due to the actions of both inertia and the Sun's force actually being continuous.
Newton (and Feynman) then proceed, from a platform of the above reasoning that a planet does indeed move and does so in a curved path (seemingly an orbit), showing Copernicus and Galileo to have been right - to prove Kepler's second law - that such moving planets 'sweep out' equal areas in equal times. Because their speed may vary according to their distance from the Sun, one might have assumed planets would sweep out a larger area in a given time when moving through their faster segments than when moving slower, but the correlation between that changing speed and the distance the planet is from the Sun (being faster the nearer it is it) means that the wider, faster sweep at the perimeter when near the Sun is associated with a shorter segment than where there is a narrow, slow sweep at the perimeter - but a longer segment - when far from the Sun. Thus, the two segments would be of equal area - as found by Kepler. However, in terms of just this 2nd law of Kepler, any variation in the speed of planets - either within a given orbit or in different orbits - as related to distance from the Sun, does not yet arise (as it will in respect of his 3rd law) and hence the validity of Kepler's findings about equal areas swept in equal times is apparently established sufficiently in terms of the following reasoning alone:
If one considers the triangle SAB (before the interval A-B is shortened at the limit into oblivion), then its area - that 'swept out' by a planet during the first time interval considered (A-B) - should equal that of the triangle SBC, swept out in the second, equal time interval B-C, and so on. This equality is proven by way of first establishing that SAB equals the triangle SBc - that swept out by a planet in the second time interval when one assumed no force was acting from the Sun - and then showing that this latter triangle also equals that of SBC, and thus that SAB equals SBC and all successive and comparable triangles swept out by a planet in equal times. Such equality of areas is shown on the basis of them having equal altitudes and a common base.
The relevance of the triangle SBc in this reasoning is fundamental and is shown as follows: A planet will sweep out equal areas of an orbit in equal times if: 1. It moves - at a constant speed - which Newton's 1st law accounts for, and: 2. It so moves in an orbit (rather than straight) - which Newton's 2nd law and his postulate about the existence and direction of a force from the Sun accounts for; ie it changes from a straight path only if another force applies and, if that new path is curved or an orbit around the Sun, such a force must be one that is directed towards the Sun; and 3. Its constant speed is not affected by that Sun-directed force (only its trajectory). If it can be shown that such a force is compatible with Kepler's 2nd law - ie that it doesn't reduce the otherwise constant speed of the planets (and their equal areas swept per equal time therefore), then both that law and the postulate concerning this directional aspect of the Sun's force are thereby verified. This is shown by the fact that the triangle SAB, which is under the influence of both inertia and gravity, is equal to (and thus not smaller than) SBc - which is affected by the former only. The strength of the Sun's force according to distance, and the consequent variation in the speed of the planet, are thus not necessary factors to consider in respect of Kepler's 2nd law which is thus proven by the foregoing geometric reasoning alone.
The fact that any of these equal triangles also equals the areas of those triangles associated with them (eg that of SBc) where no force from the Sun was assumed, has its own significance in physics in that it implies that the addition of the Sun's force, while affecting the trajectory from eg Bc to BC, does not affect the area swept out during the given time interval - an area that was later found to be proportional to a physical property called 'angular momentum'. This is affected only by forces acting across it, not by one acting perpendicular to it - as that of the Sun - which remains neutral in this regard despite its crucial effect on the planet's trajectory per se.
Having succeeded in proving Kepler's second law (that planets sweep out equal areas in equal times), the Goodsteins pause at this point to review just how this was done. As already noted above - use was made of: 1. Newton's first law (of inertia); ie once initiated, planets do move and would continue to do so - in a straight direction - given no other forces acting on them; 2. Newton's second law (any change in motion is in the direction of an additional impressed force) - ie planets actually move in a curved path - seemingly around the Sun; and 3. Newton's postulate that the source (and direction) of this additional force is thus (towards) the Sun. Nothing else. That is, to this point, there has been no need to invoke the idea or hypothesis that the strength of the force of the Sun's gravity changes (weakens) rapidly with distance (specifically as the inverse square of the distance). Kepler's second law is not dependent upon this suspected characteristic of gravity, nor on the speed of a planet. All that is needed as part of the proof is that there is a force of some kind pulling an otherwise straight-moving planet toward the Sun - whatever any variation in its strength across distance may or may not be - and that this force has no effect upon the areas swept perpendicular to this per given time - this being due solely to the constancy of the other factor effecting the otherwise straightness of its motion - inertia. Newton's first two laws, if correct, thus account for Kepler's observations of equal areas swept by a planet in equal times when applied in conjunction with a force acting on the planet that is directed (pulling) toward the Sun. The need and existence of such a force was deduced from the application of Newton's laws to the empirical findings underlying Kepler's 2nd law.
They then discuss just where the inverse square law and variations in distance and speed do prove relevant and how that law was derived. It was, in fact, deduced from Kepler's third law - which does concern the time different planets take to complete their orbits - being a function of a measure of their respective distances from the Sun - namely of the radius (or its equivalent) of their orbit - raised to the power 3/2. This measure, rather than the exact planet-to-Sun distance per se, is used as the latter is a variable value for an elliptical orbit, with the Sun at one of the focal points. The time for each orbit is thus proportional to half the distance of an orbit's semimajor axis (like its radius but along the longer axis) raised to this power of 3/2. Where one planet's orbit has a semimajor axis twice the length of another planet, its orbit will thus take 2 times as long, raised to the power of 3/2, to be completed; that is, the square root of 2 cubed (ie of 8) which = 2.83 approx - or almost 3 times as long. This law holds true whether the orbits are obvious ellipses or even if they were the special case of the 'circular ellipse' - ie where the two focal points coincide and both the semiminor and semimajor axes equals a circle's radius exactly. Thus, a distant planet, even if in a (large) circular orbit, would move more slowly than one with a (smaller) orbit nearer the Sun (whatever its shape). And if the larger orbit is, say, double the size of a smaller one, its speed is not just twice but almost three times as slow.
The proof that Kepler's third law (concerned with orbital time) allowed Newton to deduce that his related concern - the strength of the Sun's force - weakens as the square of the distance between it and a planet, occupies 12 closely argued pages of geometry by the Goodsteins . A key element in the argument, is the use not only of positional (spatial) diagrams, but velocity. diagrams derived from them. I shall not attempt to reproduce this proof here (any reader is recommended to read the the Goodsteins' book) but will simply repeat their closing statement that 'if the orbital time T for a planet is, as Kepler's third law asserts, proportional to its distance R from the Sun , raised to the power of 3/2, then that for a planet with an orbit twice that of another would (as mentioned above) be not twice but 2.83 times as long. The magnitude of the force of gravity of the Sun is proportional to R - divided by T squared - and since T = R to the power 3/2, then T squared = the square of the latter which = R cubed. Thus, the magnitude of gravity is proportional to R/R cubed, which equals 1/R squared; that is, gravity is inversely proportional to the square of the distance concerned. [Velocity diagrams are again used in the final part of the proof - ie concerning Kepler's 1st law; see below.] Thus, as with Kepler's 2nd law, this 3rd law appears to have been accounted for by the application of Newton's laws providing he could again apply a further deduced feature of gravity - on this occasion that it was a force which weakened - as the inverse square of the distance between the Sun and planet concerned. This was a deduction which Kepler's findings (regarding the relationship of a planet's speed with its distance from the Sun) pointed to, at least in Newton's mind, when he attempted to account for those findings in terms of his own 3 laws. It could now be argued that Kepler's findings regarding the orbital times being a function of the planet's distance from the Sun (raised to the power of 3/2) was necessarily the case because of the more fundamental reality of the inverse square law deduced by Newton (albeit later). [Was it at this stage that Newton required a method to calculate velocities at each point in an orbit - in order to determine the varying strength of forces acting throughout the orbit? And did this method not rely on his invention of the calculus??]
The Goodsteins usefully pause here again to review what's been achieved and where they hope to go. First, they re-state the difference between Kepler's three empirical 'laws' and those general principles/rules/laws of nature of Newton: Kepler's are generalisations based on samples of empirical data that he carefully observed and analysed. This is how nature actually behaves. Newton's are assumptions or hypotheses about the 'innermost nature of physical reality' - ie abstract principles - suggested to him by Kepler's specific empirical findings. That is, he concluded what were the most likely general causes of that carefully observed particular behaviour of nature. If the behaviour deducible from those assumptions continue to be observed in nature more generally, then the hypothesised principles of nature (true laws) may well be correct. While it may be theoretically possible for Newton or someone like him to have formulated his laws from more meagre clues from nature and to then predict planetary data and generalisations such as produced by Kepler, one feels that such hypotheses or laws would, in practice, never have been so formulated without the very empirical data they alone could subsequently account for. Thus, when demonstrating that his laws would predict elliptical orbits, Newton appears to have accepted the validity of such observed orbits as part of the rationale of formulating his universal laws.
In more detail, it is then pointed out that in order to determine the motions that planets would assume in accordance with his new laws (ultimately that they should indeed be elliptical orbits as described by Kepler's first law), Newton had first to discover more precisely the nature or properties of the force emanating from the Sun - ie gravity. Conveniently, he was able to do this (as shown above) thanks to Kepler's second and third laws combined with his own. With the nature of gravity thus revealed, he was then in a position to show that such a force of (the Sun's) gravity (viz: one directed towards the Sun and weakening as the inverse of the square of the distance between it and any planet), acting in accord with his 3 laws, would (must) result in the elliptical orbits observed by Kepler, as described in the latter's 1st law. This would provide the crucial final piece of the puzzle on which confirmation of the validity of all three of Newton's laws depended. The development of these steps is further elaborated by the Goodsteins at this point. [This seems to entail some repetition of preceding arguments.] Thus, they re-state that Newton's first law of inertia accounts for the on-going constant speed of any moving body - its mysterious 'inner force', said Newton - and his second law, coupled with the directional postulate of gravity, then accounts for the noted diversion in direction at that constant speed as some added force - from the Sun - is applied over a given time - the change in direction being towards the Sun. But the change in velocity becomes more than just a change in direction when the variability of the strength of that force is also considered. Kepler's 3rd law indicates that velocity changes throughout the orbit reflect changes in a planet's speed in different parts of the orbit and are proportional to the varying strength of the force at those points. While gravity's effects may thus reduce (be weaker) with increasing distance, Feynman (and the Goodstein's) point out (oddly without any discussion or development) that it also depends upon the time over which it acts. The effect of a strength of two units of such force over one unit of time is the same as that of one unit of force over two units of time. Finally, because of Newton's third law (about which there is again little discussion), such a force (conveniently) acts overall as though its origin and its application were concentrated at the centre points of the bodies concerned. [Convenient, because this allows the geometric analysis and proof to proceed more efficiently; its validity and this efficiency may, of course, be a reflection of some reality or truth of nature.]
By the above means, Kepler's latter two laws provided Newton insight into the nature of the Sun's force of gravity - eg the constancy of its direction of action towards the Sun and the variability of its strength according to the distance to a given planet. How might a force of just this dual nature, when acting in accordance with Newton's laws, predict that planetary orbits should indeed be elliptical - as actually found by Kepler and described in his important first 'law' (and thereby verify Newton's laws, as well as explain why Kepler found what he did)? As stated above, the answer to this final crucial question was given by Newton in 1687 by a geometrical method that is too obscure in its methodology to be readily understood today. However, Feynman, having some insight into what Newton was about, produced an alternative line of reasoning which proves more acceptable and comprehensible today (although still rather complicated!).
In this alternative, Feynman replaces Newton's idea of dividing orbits into imaginary segments that take equal times with that of segments that make equal angles 'at' the Sun (described below). Newton's segments each have the diagonal of the parallelograms at their base that represents the combined effects of the two forces acting on the planet as it orbits the Sun (as described earlier). As these equal time intervals are made shorter and shorter, so the orbits assumes less and less the shape of a polygon (of those short base lines) and more and more that of the smooth curve of the actual orbit - one which sweeps out equal areas in equal times (with a line from the planet back to the Sun). Planets nearer the Sun thus move faster than those in orbits farther from the Sun AND (say the Goodsteins, following Feynman), any given planet whose orbit is an ellipse (or at least eccentric) will move faster in that part of its orbit nearer the Sun than when it is farther from it (an ellipse being one such orbit which implies such an off-centred position for the Sun). Newton (and Feynman) appear to proceed from this point as though stating "if we assume that the orbit IS an ellipse, then we would expect the following to apply and if we find it does, we may then accept (until, if ever, proven otherwise) that it is indeed an ellipse...".
In such an (accepted) elliptical orbit, the slow moving planet at its furthest point, while covering only a short portion (arc) of its orbit because of its slow speed, would sweep an area back to the distant Sun that is equal to that swept at a faster speed (over a greater portion of arc) where the distance of the two lines of that 'sweep' - to the near Sun - are necessarily much shorter - ie long and narrow = short but broad areas - ie as described above in conjunction with Kepler's 3rd law. In his alternative proof, Feynman replaces the concept of equal areas which have such contrasting lengths of distance with that of equal angles (at the Sun) which face or oppose conversely contrasting lengths of time. The common factor between these two variables is of course the velocity or speed of the orbiting planet. The equal angles concerned are those created with lines crossing the mid-point of the Sun which run between the orbit's perimeter and define segments of time taken by an orbiting planet at its two extremes - a short time segment nearest the Sun, when the planet moves fastest, and a longer one when furthest from it, when its speed is slowest.
The two opposing segments have equal central angles but sweep out very different areas. They thus take different amounts of time, as the times taken are proportional to the areas. For example, where the time taken is half that of a slower segment, the latter's area becomes 2 x 2 = 4 times as large as the former. (In the above diagram, the segments shown on the perimeter again represent distance and the different amounts of time taken to cover such must be imagined.) In general, the area of any segment and the time taken for a planet to cover that portion of the orbit is proportional to the square of the distance from the planet to the Sun. The areas covered and times taken thus increase rapidly with distance as, say, 2, 4, 16, 256, etc. It may be recalled that the strength of the force of gravity centred on the Sun decreases similarly rapidly with the inverse square of the distance - as 256, 16, 4, 2, etc. It may be appreciated that when analysing geometric data which have several mutually affecting variables such as time, distance, velocity, angles, velocity changes and areas, one can proceed by holding particular variables constant while examining the effects on others allowed to vary. Newton analysed Kepler's data by holding time intervals constant (among other things) while Feynman sought to hold velocity changes constant (among other things). Their ultimate equivalence is apparently assumed.
The planet's orbit is changed from that due to its inertia alone (straight with constant velocity) to some kind of curved orbit depending on the strength of the force from the Sun and the length of time that force is acting on it. This implies that the change in velocity is not dependent upon the distance the planet is from the Sun per se but rather on force and time alone - the weakening effect of the former at a long distance being exactly compensated for by the longer duration of action due to the latter and vice versa. Because these are a function of the areas swept out, the changing velocities for successive identical angles with the Sun are all the same - all the way around the orbit. If the angles through which the orbit moves are not equal, the changes in velocity will also vary accordingly and with them, the shape of the orbit - compared with that of a constant change in velocity. That is, from that of a circle apparently - to that of, say, an ellipse.
As Newton described a planet's orbit (in the earlier part of his proof), the time intervals of each segment were identical and the added force towards the Sun caused successive changes in velocity to all be in that direction, but with greater changes occurring where the orbit was nearer the Sun - causing a 'sharper' curve there (as with Mercury or any planet when nearer the Sun); that is, the velocity changes are all different in each successive equal time interval. This leads to an irregular polygon which, if the equal time intervals are made progressively shorter, becomes a smooth non-circular orbit - as an ellipse - in the limit. But in Feynman's scheme, the time intervals of successive segments are all different because they are based on equal central angles instead (the equality in one implying an inequality in the other and vice versa), so now the velocity changes are all the same all the way around the orbit, each occurring over equal angles of movement (but at different speeds) - though still pulling towards the Sun as required by Newton's 2nd law. In this case, when the equal angles are the variable which become progressively smaller, the regular polygon produced must now becomes a circle at the limit.
The proof continues with a very detailed analysis of the geometric arguments based upon relevant variables such as time, distance, velocity changes, etc. The Goodstein's point out that Newton reasoned his way towards his final conclusions by means of various lines of thought which only gradually formulated themselves into his final 3 laws. We have the advantage now of idealising this process into a more concise form. Thus, one can assume that his thinking went along certain lines which approximate the following: 'Because planets sweep out equal areas in equal times, I can apply the laws of inertia, force and action/reaction to deduce that the force of the Sun's gravity on a planet is directed towards the (centre of the) Sun. Then, because the time for a planet to complete its orbit is proportional to the 3/2 power of its distance from the Sun, these same laws allow me to conclude that such gravity diminishes in strength as the inverse square of that distance. Finally, knowing and applying this dual nature of gravity, the laws support the finding of Kepler that such orbits are ellipses. And hence, the validity of these three laws is fully supported and should continue to be accepted until and unless any other data should ever materialise to the contrary. For all practical purposes, they still hold today - three hundred years later. Only at the sub-atomic level and at or near the speed of light have the later discoveries of Einstein's relativity and Bohr's quantum mechanics required some adjustments to Newton's conception of the universe. In fact, it still holds true as a limiting case and as a most significant part of these more general models of nature.
Thus, the Goodstein's point out also that, importantly, Newton's laws "..explained not only the motions of the planets but almost every other phenomenon in the physical world as well". For they are concerned with how all matter behaves (moves) when acted upon by forces. Whatever happens in this universe entails the movement of matter by forces. While science is still seeking to understand fully just what both matter and forces actually are, knowing what they do, and how they interact, is a necessary and fundamental first step. The reorganisation of our understanding of the universe, both in space and here on Earth, as discovered by Newton, began with the proof of Kepler's elliptical orbits. As brilliant as his discovery of them was, the latter could not account for or explain them. Newton did - in terms of his three fundamental laws of nature.
P.S. We may ask 'How and where would Newton's ideas on absolute vs relative motion fit into the foregoing'? Were these ideas relevant to the developments in Physics from this foundation of mechanics over the next century? Also, we might usefully enquire more into the need for Newton to develop his conception of the differential and integral calculus - seemingly needed to ascertain the values of changing velocities/accelerations at precise points in any orbit in order to establish the strength and direction of the forces applying - and hence identify/confirm their apparent origins. This was apparently not possible by simply analysing the overall, orbit shapes/trajectories; it was the size and source of the forces acting point by point as the orbit changed that held the key to knowing that F = ma and what was behind that. The integral calculus would allowed him to sum up the infinitesimal bits of the orbit of a planet and conclude that with the Sun's gravity acting on these, the orbits must be ellipses. Parabolas and hyperbolas are other possible trajectories (ie as per conic sections) and depend on the strengths of the component forces so acting. With the initial velocity given to all planets, they become ellipses. Objects given lesser initial velocities but still being acted on as well by gravity, as a canon ball, will show a parabolic trajectory. Is an exact circular orbit possible? Knowing the initial conditions (velocities/forces and positions/directions) of any and every object/particle it should in theory be possible to predict the future - but quantum mechanics claims this is not so; see later. In the meantime, the electromagnetic world as per Faraday and Maxwell, meant that pure classical mechanics alone was insufficient to account for all phenomena - a new synthesis of these was needed. These aspects too are touched on later - in the main account on Relativity.
Addendum
The following is added in the event it might provide (me with) some insight into the relevance of conic sections to the dynamics of moving bodies (as per the 'alchemy' referred to earlier):
The velocity diagram as used by Feynman in his proof (but used earlier by the great Clerk Maxwell in 1877, who attributed its development to another Scots genius - Sir William Hamilton) apparently always assumes a circular shape when the inverse square law of gravity and Newton's 3 laws of mechanics are applied to any object orbiting a much larger one. The shape of the orbit depends on where the origin of the velocity diagram is. There are 4 possible categories for this position and, intriguingly, these lead to 'orbits' which represent the 4 conic sections - ie the circle, ellipse, parabola and hyperbola. As Newton used a sequence of reasoning in the latter part of his original proof which entailed obscure use of these sections, it would seem to follow that Feynman's method may well have relied implicitly on the same essential logic - albeit approached from a different perspective.
Thus, if the origin coincides with the centre of the velocity circle then the two foci of the orbit coincide also and produce a circle - where the orbiting body's speed would remain the same throughout. Secondly, the origin can occur anywhere between the centre point and the perimeter of the diagram in which case the orbit becomes an ellipse. This will be almost circular, with the two foci relatively close, where the origin of the velocity circle is close to its centre point. When the origin is nearer to the perimeter however, a very elongated ellipse will arise - as in the case of many comets. In our solar system, most planetary orbits are near circular ellipses with the distance between the foci accounting for only a small percent of the longer diameter (between 1 and 20 % compared to the 97% for Halley's comet). Nevertheless, the speed varies in such orbits as per Kepler's laws. Presumably, Feynman (and likewise Newton) chose an origin in accordance with Kepler's actual findings (of varying speed and direction) which resulted in the elliptical orbit found and proved.
Thirdly, the origin could be outside the circle. This eventually produces a change in velocity which is in the same direction as the velocity itself - that is, the 'orbiting' body ceases to change direction but tends towards a straight line as it moves away from its focus. Its trajectory is thus that of a hyperbola beginning and ending in infinity (as it were) but apparently never having a zero velocity. Finally, the origin could be on the circle itself (thus exceeding even the eccentricity of an extreme comet), in which case, its trajectory becomes a parabola in which its velocity 'at the limit' does become zero. How such a body could in practice begin its journey (from such a zero velocity), I'm presently unaware!
To 'The Background To The Problems Addressed By Einstein...'